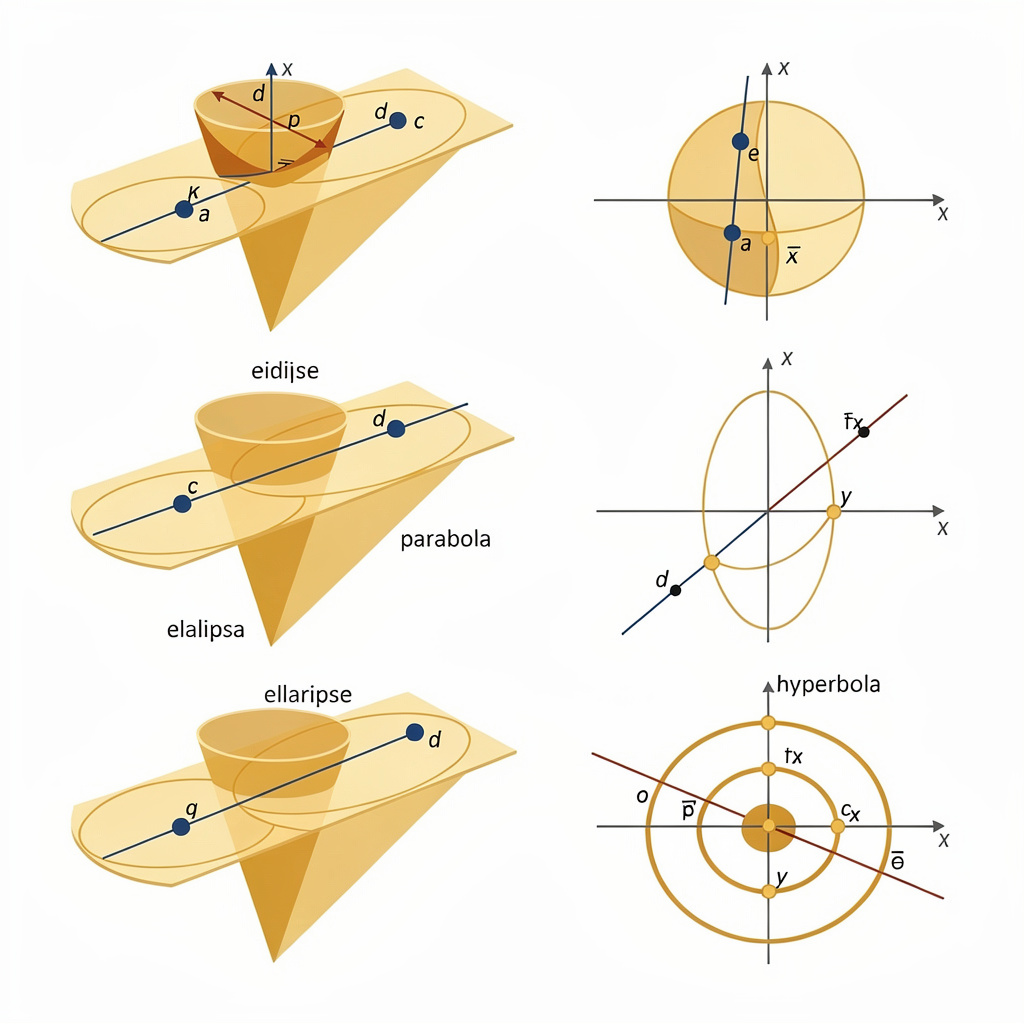
As cônicas são curvas planas obtidas pela interseção de um plano com um cone circular reto. Esse estudo inclui a elipse, a hipérbole e a parábola, além da circunferência como caso especial. As cônicas têm aplicações importantes em física, astronomia e engenharia.
As órbitas dos planetas são elipses, as trajetórias de cometas podem ser parabólicas ou hiperbólicas, e as cônicas aparecem em problemas de reflexão e antenas parabólicas. Nesta lista de exercícios, você dominará as equações e propriedades de cada cônica.
Elipse
A elipse é o lugar geométrico dos pontos cuja soma das distâncias a dois pontos fixos (focos) é constante. Sua equação reduzida com centro na origem é x²/a² + y²/b² = 1, onde a > b. A relação entre os semieixos é c² = a² – b², onde c é a distância focal.
Hipérbole
A hipérbole é o lugar geométrico dos pontos cuja diferença das distâncias aos focos (em módulo) é constante. Sua equação é x²/a² – y²/b² = 1 (eixo real horizontal) ou y²/a² – x²/b² = 1 (eixo real vertical). A relação é c² = a² + b².
Parábola
A parábola é o lugar geométrico dos pontos equidistantes de um ponto fixo (foco) e uma reta fixa (diretriz). Suas equações principais são y² = 4px (eixo horizontal) ou x² = 4py (eixo vertical), onde p é a distância do vértice ao foco.
Pratique com Nossa Lista de Exercícios
Agora que você revisou os conceitos sobre cônicas, chegou a hora de praticar! Nossa lista de exercícios foi elaborada com questões de vestibulares para você dominar esse importante tópico.